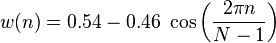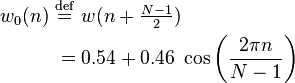Window function

High- and moderate-resolution windows

Rectangular window

Rectangular window; B=1.00

$w(n) = 1\,$

The rectangular window is sometimes known as a Dirichlet window. It is the simplest window, taking a chunk of the signal without any other modification at all, which leads to discontinuities at the endpoints (unless the signal happens to be an exact fit for the window length, as used in multitone testing, for instance). The first side-lobe is only 13 dB lower than the main lobe, with the rest falling off at about 6 dB per octave.

Hann window

Hann window; B = 1.50

Main article: Hann function

$w(n) = 0.5\; \left(1 - \cos \left ( \frac{2 \pi n}{N-1} \right) \right)$

Note that:

$w_0(n) = 0.5\; \left(1 + \cos \left ( \frac{2 \pi n}{N-1} \right) \right)$

The ends of the cosine just touch zero, so the side-lobes roll off at about 18 dB per octave.

The Hann and Hamming windows, both of which are in the family known as "raised cosine" windows, are respectively named after Julius von Hann and Richard Hamming. The term "Hanning window" is sometimes used to refer to the Hann window.

Hamming window

Hamming window; B=1.37

The "raised cosine" with these particular coefficients was proposed by Richard W. Hamming. The window is optimized to minimize the maximum (nearest) side lobe, giving it a height of about one-fifth that of the Hann window, a raised cosine with simpler coefficients.

$w(n) = 0.54 - 0.46\; \cos \left ( \frac{2\pi n}{N-1} \right)$

Note that:

$\begin{align} w_0(n)\ &\stackrel{\mathrm{def}}{=}\ w(n+\begin{matrix} \frac{N-1}{2}\end{matrix})\\ &= 0.54 + 0.46\; \cos \left ( \frac{2\pi n}{N-1} \right) \end{align}$

Tukey window

Tukey window, α=0.5; B=1.22

$w_0(n) = \left\{ \begin{matrix} \frac{1}{2} \left[1+\cos \left(\pi \left( \frac{2 n}{\alpha N}-1 \right) \right) \right] & \mbox{when}\, 0 \leqslant n \leqslant \frac{\alpha N}{2} \\ [0.5em] 1 & \mbox{when}\, \frac{\alpha N}{2}\leqslant n \leqslant N (1 - \frac{\alpha}{2}) \\ [0.5em] \frac{1}{2} \left[1+\cos \left(\pi \left( \frac{2 n}{\alpha N}- \frac{2}{\alpha} + 1 \right) \right) \right] & \mbox{when}\, N (1 - \frac{\alpha}{2}) \leqslant n \leqslant N \\ \end{matrix} \right.$

The Tukey window, also known as the tapered cosine window, can be regarded as a cosine lobe of width $\tfrac{\alpha N}{2}$ that is convolved with a rectangle window of width $\left(1 -\tfrac{\alpha}{2}\right)N$ . At α=0 it becomes rectangular, and at α=1 it becomes a Hann window.

Cosine window

Cosine window; B=1.24

$w(n) = \cos\left(\frac{\pi n}{N-1} - \frac{\pi}{2}\right) = \sin\left(\frac{\pi n}{N-1}\right)$

also known as sine window
cosine window describes the shape of $w_0(n)\,$

Lanczos window

Sinc or Lanczos window; B=1.31

$w(n) = \mathrm{sinc}\left(\frac{2n}{N-1}-1\right)$

used in Lanczos resampling
for the Lanczos window, sinc(x) is defined as sin(πx)/(πx)
also known as a sinc window, because:

$w_0(n) = \mathrm{sinc}\left(\frac{2n}{N-1}\right)\,$ is the main lobe of a normalized sinc function

Triangular windows

Bartlett window; B=1.33

Bartlett window with zero-valued end-points:

$w(n)=\frac{2}{N-1}\cdot\left(\frac{N-1}{2}-\left |n-\frac{N-1}{2}\right |\right)\,$

Triangular window; B=1.33

With non-zero end-points:

$w(n)=\frac{2}{N}\cdot\left(\frac{N}{2}-\left |n-\frac{N-1}{2}\right |\right)\,$

Can be seen as the convolution of two half-sized rectangular windows, giving it a main lobe width of twice the width of a regular rectangular window. The nearest lobe is -26 dB down from the main lobe.

Gaussian windows

Gauss window, σ=0.4; B=1.45

The frequency response of a Gaussian is also a Gaussian (it is an eigenfunction of the Fourier Transform). Since the Gaussian function extends to infinity, it must either be truncated at the ends of the window, or itself windowed with another zero-ended window.

Since the log of a Gaussian produces a parabola, this can be used for exact quadratic interpolation in frequency estimation.

$w(n)=e^{-\frac{1}{2} \left ( \frac{n-(N-1)/2}{\sigma (N-1)/2} \right)^{2}}$

$\sigma \le \;0.5\,$

Bartlett–Hann window

Bartlett-Hann window; B=1.46

$w(n)=a_0 - a_1 \left |\frac{n}{N-1}-\frac{1}{2} \right| - a_2 \cos \left (\frac{2 \pi n}{N-1}\right )$

$a_0=0.62;\quad a_1=0.48;\quad a_2=0.38\,$

Blackman windows

Blackman window; α = 0.16; B=1.73

Blackman windows are defined as:

$w(n)=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N-1} \right) + a_2 \cos \left ( \frac{4 \pi n}{N-1} \right)$

$a_0=\frac{1-\alpha}{2};\quad a_1=\frac{1}{2};\quad a_2=\frac{\alpha}{2}\,$

By common convention, the unqualified term Blackman window refers to α=0.16.

Kaiser windows

Kaiser window, α =2; B=1.5

Kaiser window, α =3; B=1.8

Main article: Kaiser window

A simple approximation of the DPSS window using Bessel functions, discovered by Jim Kaiser.

$w(n)=\frac{I_0\Bigg (\pi\alpha \sqrt{1 - (\begin{matrix} \frac{2 n}{N-1} \end{matrix}-1)^2}\Bigg )} {I_0(\pi\alpha)}$

where $I 0$ is the zero-th order modified Bessel function of the first kind, and usually $α = 3$ .

Note that:

$w_0(n) = \frac{I_0\Bigg (\pi\alpha \sqrt{1 - (\begin{matrix} \frac{2 n}{N-1} \end{matrix})^2}\Bigg )} {I_0(\pi\alpha)}$

Low-resolution (high-dynamic-range) windows

Nuttall window, continuous first derivative

Nuttall window, continuous first derivative; B=2.02

$w(n)=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N-1} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N-1} \right)- a_3 \cos \left ( \frac{6 \pi n}{N-1} \right)$

$a_0=0.355768;\quad a_1=0.487396;\quad a_2=0.144232;\quad a_3=0.012604\,$

Blackman–Harris window

Blackman–Harris window; B=2.01

A generalization of the Hamming family, produced by adding more shifted sinc functions, meant to minimize side-lobe levels

$w(n)=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N-1} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N-1} \right)- a_3 \cos \left ( \frac{6 \pi n}{N-1} \right)$

$a_0=0.35875;\quad a_1=0.48829;\quad a_2=0.14128;\quad a_3=0.01168\,$

Blackman–Nuttall window

Blackman–Nuttall window; B=1.98

$w(n)=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N-1} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N-1} \right)- a_3 \cos \left ( \frac{6 \pi n}{N-1} \right)$

$a_0=0.3635819; \quad a_1=0.4891775; \quad a_2=0.1365995; \quad a_3=0.0106411\,$

Flat top window

Flat top window; B=3.77

$w(n)=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N-1} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N-1} \right)- a_3 \cos \left ( \frac{6 \pi n}{N-1} \right)+a_4 \cos \left ( \frac{8 \pi n}{N-1} \right)$

$a_0=1;\quad a_1=1.93;\quad a_2=1.29;\quad a_3=0.388;\quad a_4=0.032\,$

728x90

저작자표시 비영리 동일조건

'AUDIO_ > Flowing_' 카테고리의 다른 글

클리펠 교육 (0)	2013.07.31
Equivalent Rectangular Bandwidth (ERB) (3)	2010.11.01
Seminar in Korea_ (2)	2010.10.20
Bob McCarthy introduces SIM 3 seminar (1)	2010.10.01
SAM BERKOW ON LINE ARRAYS (1)	2010.08.03

기꺼이 하는일엔 행운이 따르죠_